现代网络理论

在 1920 年代初,Otto Zobel 和 George Campbell 发明了一种滤波器设计方法, 称为图像参数设计. 这提供了一种相对简单的方法来设计使用级联各种构建块电路的滤波器,每个构建块电路都有一个相关的响应. 最终设计需要通过镜像阻抗进行端接(源和负载). 这个阻抗等于查看网络时看到的阻抗. 但是, 包含电感器和电容器的网络的输入和输出阻抗是频率的复杂函数, 而不仅仅是电阻. 在现实世界中, 滤波器在固定电阻值之间运行, 因此想让网络终端输出具有复阻抗是不切实际的 . 本书将专注于现代网络理论, 也称为插入损耗法. 该方法从多项式族开始, 这些多项式近似于滤波器特性. 可以从这些多项式合成在定义的电阻器之间运行的滤波器. 本章将给出几个简单的例子.

广义滤波器如Fig1.1, 波器块可以由电感器,电容器,电阻器和可能的有源元件组成, 例如运算放大器和晶体管. 所示的终端是电压源 Es, 源电阻Rs和负载电阻器RL.

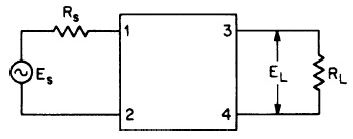
Fig.1.1. 网络的电路方程可以用电路分析技术写出来. 现代网络理论通过求解这些方程来确定在某些方面实现最佳性能的网络值.

1.1.零极点概念

广义滤波器的频率响应可以表示为 s 的两个多项式的比值,称为传递函数. 其中s=jω(j=(-1)^0.5, ω=2πf为弧度每秒).

$\displaystyle T(s)= \frac{E_L}{E_S}= \frac{N(s)}{D(s)} \qquad (1.1)$

分母多项式D(s)的根称为极点, 分子多项式 N(s)的根称为零点.

推导网络的传递函数可能会相当乏味, 超出了本书的范围. 此外, 滤波器的成功设计不需要零极点理论的知识. 然而, 这个概念很重要, 它可以让设计人员了解各种滤波器类型之间的差异以及所涉及的一些敏感性.

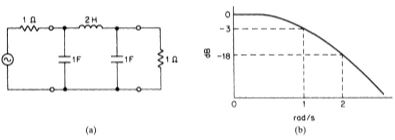
下面的讨论关乎一个相对简单的传递函数的评估和表示. 分析Fig1.2a的低通滤波器得到如下传递函数：

$\displaystyle T(s) = \frac{1}{s^3+2s^2+2s+1} \qquad (1.2)$

现在让我们在用 jω 代替 s 之后在不同的频率下评估这个表达式. 结果将表示为 T(jω)的绝对幅度和相对于 DC 响应的相对衰减(以分贝为单位).

$\displaystyle T(j \omega) = \frac{1}{1-2\omega^2 +j(2\omega-\omega^3)} \qquad (1.3)$

ω	\|T(jω )\|	20log\|T(jω )\|
0	1	0 dB
1	0.707	-3 dB
2	0.124	-18 dB
3	0.0370	-29 dB
4	0.0156	-36 dB

Note:频响曲线见Fig.1.2b

对Eq(1-2)的分析表明, 传递函数的分母有三个根或极点, 而分子没有0点. 因此,该滤波器被称为全极型. 由于分母是三阶多项式, 因此滤波器的复杂度也称为 n = 3. 分母极点是 s = –1, s = –0.500 + j 0.866, s = –0.500 – j 0.866.

这些复数可以表示为复数平面上的符号. 横坐标是α, 即根的实部, 纵坐标是β, 即虚部. 每个极点用符号 X 表示,零表示为 0. Fig.1-3 展示了Eq.(1-2)的根的复数平面表示.

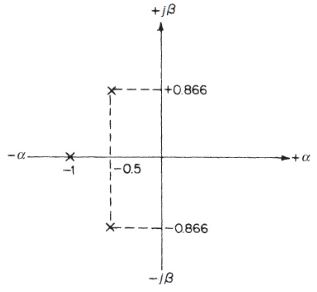
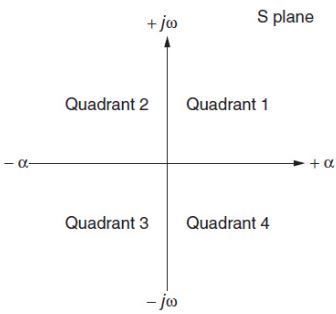
Fig.1.4展示了复数平面的一般形式,我们将其称为 S 平面,因为它基于 s 的多项式的根. 注意有四个象限, 因为负频率不存在, 它只是一个数学概念, 所以我们只关注象限 1 和 2.

现在让我们考虑更复杂的传递函数如下:

$\displaystyle T(s) = \frac{s+1}{(s^2+4s+5)(s^2+2s+5)} \qquad(1.4)$

Eq(1.4)的分母可分解为如下4项.

$\displaystyle T(s) = \frac{s+1}{(s+2+j)(s+2-j)(s+1+j2)(s+1-j2)} \qquad(1.5)$

S平面中的零在分子为0的解, 即s =–1. S 平面中的极点是分母为零的点,即:

s=-2-j1

s=-2+j1

s=-1-j2

s=-1+j2

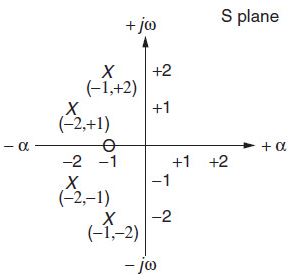
如果s为上述根中的任何一个, T(s)的分母为0, 根将为无穷大. Eq.(1.5)的极点和0点如Fig.1.5的S平面.

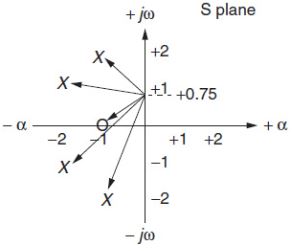
要直接从S平面确定频率响应的幅度, 请绘制从感兴趣频率到每个极点和零点的矢量. 如Fig.1.6所示, 感兴趣频率为0.75 rad/s. 频率响应的幅度是从感兴趣的频率到零点的所有向量长度的乘积除以从感兴趣的频率到极点的所有向量的乘积.(读起来比较拗口, 大体就是到0点的向量长度做分子, 到极点的向量长度做分母)

为了计算相位,将向量与零点的所有角度相加, 然后从该数字中减去所有极向量的角度总和.

请注意, 如果极点的实部很小, 则极点会对极点虚部附近的频率响应产生剧烈影响. 极点的实部越小, 它对响应的影响就越大, 并且当它的虚部接近 jw 轴时会导致峰值效应.

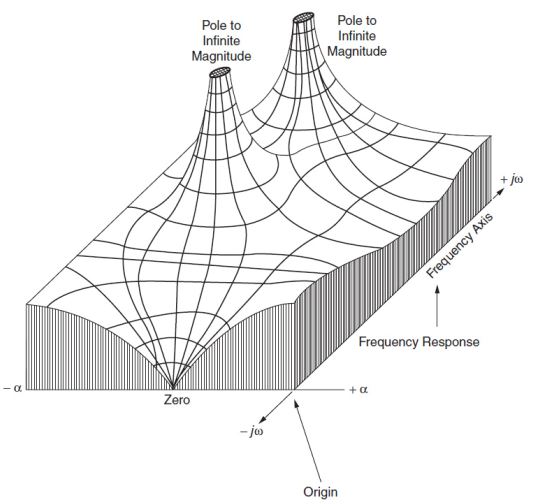
Fig.1.7所示, 一个“马戏团帐篷”类比 S 平面中的极点和零点. Zeros 类似于“帐篷桩”, 其中帐篷的高度为零. Poles就像“帐篷杆”, 但有无限的高度. 如果你如图所示切掉一段, 你会看到一个受极点和零点影响的形状.

为了实现滤波器, 对极点和零点的位置有一定的数学限制. 它们必须成对出现,彼此共轭, 实轴极点和零点除外, 它们可能单独出现. 极点也必须限制在左平面(即极点的坐标实部必须为负). 零点可能出现在任一平面中. 传递函数的分子的阶次不能比分母高. 换句话说, 零点不能多于极点. 极点也不能在 jw 轴上, 因为这意味着 T(s)的值是无限的,这将是一个振荡条件; 即,没有输入也会产生无限的输出.

让我们再考察一个S平面示例. 带通滤波器在第5章中有广泛的介绍, 但在这里检查零极点模式及其对二阶带通滤波器行为的影响会很有用. 二阶带通传递函数可以表示为:

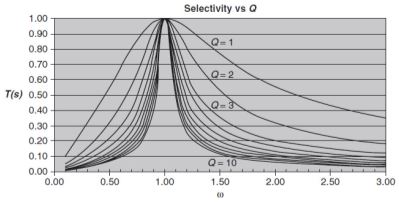
$\displaystyle T(s) = \frac{s}{s^2+\frac{\omega_0}{Q}s+\omega^2_0} \qquad(1.6)$

Q,也称为选择性因子, 是用于表示极点和带通滤波器的“选择性”的术语. (有时 Q 定义为中心频率除以 3-dB 带宽.) Fig.1.8表示一个二极点带通滤波器, 其零点位于原点处, 如Eq.(1.6) 所述.

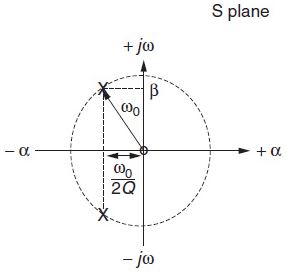
中心频率为 ωo, 极点 α 的实部为 ωo/2Q. 因此 Q 是 ωo/2α. 这意味着极点 (a) 的实部越小, Q 或选择性因子就越高. 极点的虚部是β. 对于高Qs, ωo接近β.

从Fig.1.8 可以清楚地看出, 随着Q的增加, 极点α的实部分量减小. 极点将更靠近 jω轴, 因此将对频率响应产生更大的影响. 如Fig.1-9所示, 在这种带通情况下, 将出现峰值(幅度增加).

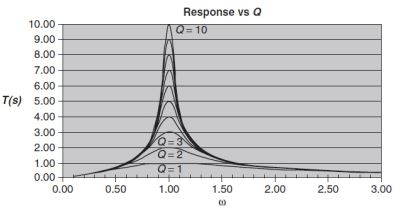
Eq.(1.6)也可以用归一化形式表示, 其中T(s)的最大值始终为 1. 这将是Eq.(1.7),相应的曲线如Fig.1.10所示.

$\displaystyle T(s) = \frac{\frac{\omega_0}{Q}s}{s^2+\frac{\omega_0}{Q}s+\omega^2_0} \qquad(1.6)$

现代网络理论

分享到：