第2章. 选择响应特性

2.1. 频响归一化

几个参数用于表征滤波器的性能. 最常见的指定要求是频率响应. 当给出频率响应规范时, 工程师必须选择满足这些要求的滤波器设计. 这是通过将所需响应转换为截止值为 1 rad/s 的归一化低通规范来实现的. 将此归一化响应与归一化低通滤波器的曲线进行比较, 后者也具有 1-rad/s 截止. 在从曲线确定令人满意的低通滤波器后, 将所选滤波器的列表归一化元素值转换或非归一化到最终设计.

现代网络理论为我们提供了许多不同形状的幅度与频率, 它们是通过对传递函数施加各种限制而分析得出的. 这些低通响应的主要类别是:

• Butterworth maximally flat amplitude
• Chebyshev
• 贝塞尔最大平坦延迟(Bessel maximally flat delay)
• 具有等波纹误差的线性相位(Linear phase with equiripple error)
• Transitional
• 同步调谐(Synchronously tuned)
• 椭圆函数(Elliptic-function)
• 帕普利斯最佳“L”(Papoulis optimum “L”)
除了椭圆函数族之外, 这些响应都归一化为 1 rad/s 的 3-dB 截止值.

2.1.1. 频率和阻抗缩放

滤波器归一化的基础是, 通过将电抗元件除以频率缩放因子(FSF, frequency-scaling factor),可以将给定滤波器的响应缩放(移动)到不同的频率范围. FSF 是所需响应的参考频率与给定滤波器的相应参考频率之比. 通常选择3-dB点作为低通和高通滤波器的参考频率,中心频率作为带通滤波器的参考. FSF 可以表示为:

$\displaystyle FSF=\frac{desired reference frequency}{existing reference frequency}$

FSF 必须是无量纲数; 所以Eq.(2.1)的分子和分母必须用相同的单位表示, 通常是弧度每秒. 以下示例演示了 FSF 的计算和滤波器的频率缩放.

示例 2-1 低通滤波器的频率缩放

要求:

一个低通滤波器(LC或有源)具有n=3巴特沃斯传递函数, 在1,000Hz处具有3dB截止.

结论:

Fig.2.1 演示了第1章中讨论的LC和有源n=3巴特沃斯低通滤波器及其响应.

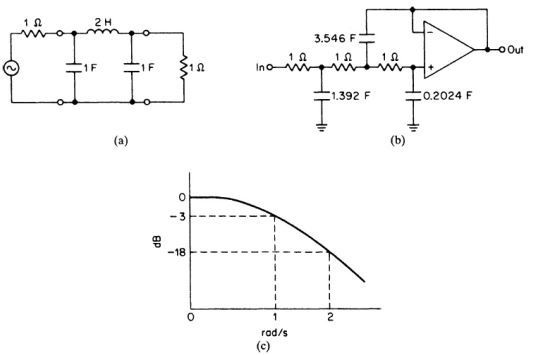
Fig.2.1.n=3 Butterworth low-pass filter:(a)LC filter,(b)active filter,(c)frequency response.

(a).使用Eq.(2.1)计算频率缩放因子

FSF=(2π*1000 rad/s)/(1 rad/s)=6280

(b).将所有电抗元件(reactive elements)除以FSF得到Fig.(2.2)a和b的滤波器以及Fig.2.2c 的响应.

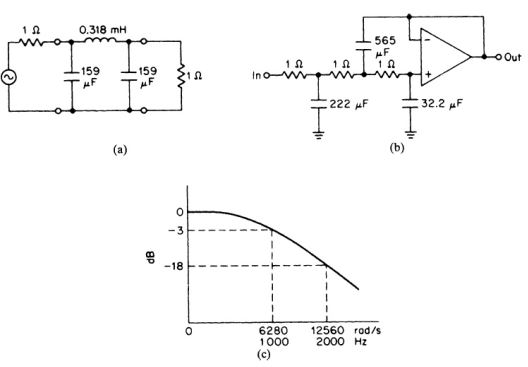
Fig.2.2.去归一化的n=3 Butterworth low-pass filter(对应Fig.2.1).

请注意, 归一化响应的频率轴上的所有点都已乘以FSF. 此外,由于归一化滤波器的截止频率为1 rad/s, 因此FSF可以直接用2πf_c表示, 其中f_c是所需的低通截止频率, 以赫兹为单位.

滤波器频率缩放具有将响应曲线的频率轴上的所有点乘以FSF的效果. 因此,可以直接使用归一化响应曲线来预测非归一化滤波器的衰减. 当Fig.2.1的滤波器被去归一化为Fig.2.2的滤波器时, 传递函数也发生了变化.去归一化传递函数变为:

T(s)=1/(4.03*10^-12s³+5.08*10^-8s²+3.18*10^-4s+1) (2.2)

分母有根:

s=-6.280, s=-3.140+j5.438, s=-3140-j5438

Matlab Code如下:

clc,clear;
syms s;
%a=1; b=2; c=2; d=1;
a=4.038810^(-12); b=5.068310^(-8); c=3.18610^(-4); d=1; e1 = as.^3+bs.^2+cs+d;
x0 = double(solve(e1,s))
c1=565e-6;c2=222e-6;c3=32.2e-6;
A=c1c2c3;
B=2c3(c1+c2);
C=c2+3*c3;

这些根可以通过将归一化根坐标乘以 FSF 直接从归一化根中获得. 滤波器频率缩放还按相同的因子缩放极点和零点(如果有).

Fig.2.2中滤波器的分量值不是很实用. 电容值太大, 1Ω 电阻值不是很理想. 这种情况可以通过阻抗缩放来解决. 如果所有电阻器和电感器值都乘以阻抗比例因子Z, 并且所有电容器除以相同的因子Z, 则任何线性有源或无源网络都保持其传递函数. 这是因为Zs在传递函数中抵消. 为了证明这一点,让我们研究Fig.2.3a的简单两极低通滤波器的传递函数, 即

T(s)=1/(s²LC+sCR+1) (2.3)

阻抗缩放可以在数学上表示为:

R’=ZR (2.4)

L’=ZL (2.5)

C’=C/Z (2.6)

其中R’,L’,C’表示阻抗缩放后的值.

如果我们对滤波器进行阻抗缩放,会得到Fig.2.3b的电路. 然后新的传递函数变为:

$\displaystyle T(s)=\frac{1}{s^2ZL\frac{C}{Z}+s\frac{C}{Z}ZR+1} \qquad(2.7)$

显然, Zs相互抵消了, 所以两个传递函数是等价的.

我们现在可以使用阻抗缩放来使Fig.2.2的滤波器中的值更实用. 如果我们使用Z为1,000的阻抗缩放, 我们得到Fig.2.4的滤波器. 这些值当然更合适.

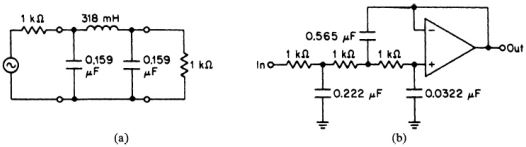
Fig.2.4.示例2.1的阻抗缩放滤波器:(a).LC 滤波器和(b).有源滤波器

频率和阻抗缩放通常合并为一个步骤,而不是顺序执行. 然后由下式给出去归一化值:

R’=RxZ (2.8)

L’=LxZ/FSF (2.9)

C’=C/FSFxZ (2.10)

其中R’,L’,C’是频率和阻抗缩放的.

第2章. 选择响应特性

分享到：