在Automatic Design对话框点击OK后, AUTO开始运行,显示出列表式的输出视窗(TOW,Tabbed output window)和一个带有STOP键的控制对话框. TOW总是有一个包括了大部分输出内容的Text列表. 如果要求每次循环都绘制一次透镜的视图,那么您就会看到多组曲线/数据列表, 每次循环一组. 如果有警告或错误产生的话, 也可以看到一个Error列表.
控制对话框显示当前的循环次数和误差函数值. 注意, 如果您点击了Stop键, AUTO不会马上停止. 它要完成当前的循环, 并且确保在停止之前透镜的数据是有效的.
3.5.1.误差函数
误差函数是在AUTO运行时所产生的最有用的一个信息. 这个数字代表了透镜的成像质量,数字0代表了一个无像差透镜. 缺省的误差函数是由X,Y方向的横向光线像差的平方和构成, 其比例的确定使得该值近似等于所有视场和变焦位置的平均后RMS光斑半径的平方. 缺省的误差函数还有波前误差方差, 光纤匹配效率和MTF. 在这些情况中,对误差函数值的解释是不同的,但是都认为越小越好, 最理想的状态是0, 但是几乎不可能达到. 也可以使用用户自定义误差函数.
为了计算误差函数, CodeV对每一个确定的视场, 变焦位置, 一种波长追迹一组光线网络. 网格定义如下: 假设入瞳的半径是1(规划值), 光线之间的间隔被认为是瞳孔上用小数点表示的光线间隔(命令:DEL). 有一个宏指令(AUTOGRID.SEQ, 可以在Tools>Macro菜单中找到,并且被列在Sample Macros/Optimization下面)可以用来检查具体的DEL值的光线分布图. 这次优化中所选取的DEL值是0.22, 光线分布图如下图所示. (注意当AUTO对话框或者其它任何选项的对话框是打开状态时, 你不可能运行该宏指令或其他任何宏指令)
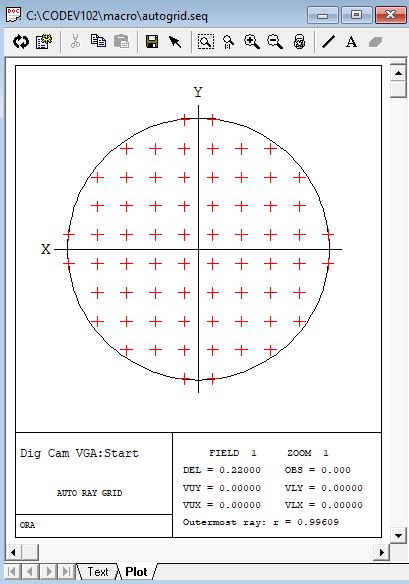
每一条光线在XY方向的横向像差都是在像面上被计算出来的,这些像差的加权平方和确定每次优化循环中误差函数的值. 求和公式中的权重对优化是一个重要的控制. 对孔径的位置, 波长和视场(X和Y分量)都要确定权重. 对于误差函数更详细的处理及优化的其他数学问题参见Reference Manual P3-80.
3.5.2.AUTO输出的标题
现在让我们看看AUTO文本输出, 输出首先是显示计算中使用的输入数据和缺省值, 这部分被称为输出标题. 主要以命令形式给出.
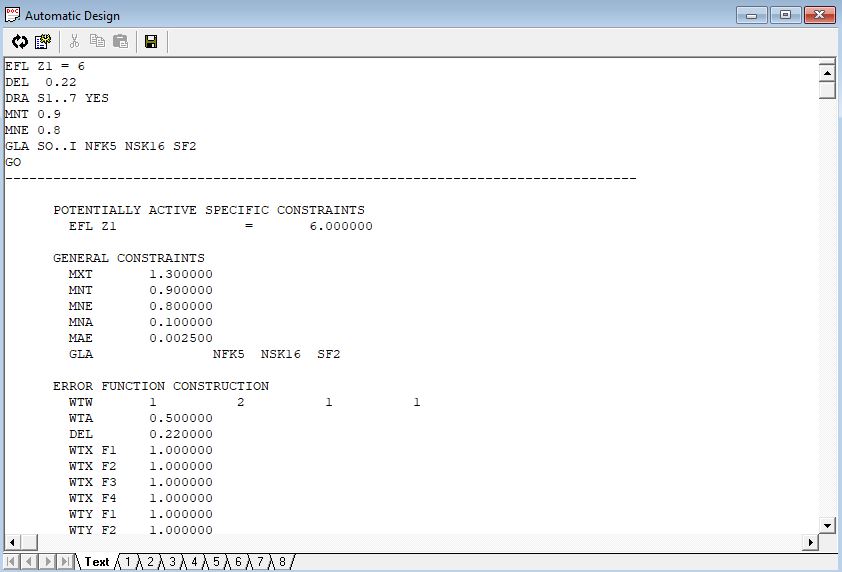
通过显示有您的设置(EFL,DEL等)所产生的命令开始输出标题. 然后,在EFL情况下, 会列出可能使用的特殊约束. “可能使用”就意味着AUTO将动态的决定每次循环时是否需要某种约束, 为了控制像差, 要尽可能多释放一些变量. 然后列出一般约束, 命令也不难理解(MNE,Minimum Edge thickness是最小边厚, MXT, Maximum center Thickness是最大中心厚度等)
提示:要查看一种输入类型的命令, 在Automatic Design对话框中点击感兴趣的选项(例如General Constraints)并按F1键, 将显示出一个描述输入的帮助页, 包括CodeV命令的名字.
Error Function Construction(误差函数结构)显示出不同项目上的权重,以及光线追迹网络中使用的DEL值.
Convergence Control(收敛控制)显示了退出的条件(MXC是最大的循环次数,MNC是最小的循环次数,TAR是误差函数的目标值,IMP是每一次循环实现的目标值提高的部分).
Output Control这个例子中, 仅仅包括透镜的绘图命令(DRA).紧接着是变量的数目,该例子中是18个变量(6个变量,6个厚度,6个玻璃变量,每个玻璃都有折射率色散2个变量).
提示:在AUTO对话框Output Controls列表的Variable Table栏中点击Print Cycle Value键, 就可以得到一个变量表.
最后, 标题的内容将告诉您,由于是18个变量, 因此18种约束可以被使用. 这是一个上限, 事实上希望使用较少的约束应用最高的自由度(即变量)来提高像质.
3.5.3.AUTO每次循环的输出
一般来说AUTO中的一次循环就是一次显示误差函数和约束的迭代. 事实上,每次循环都会包含几次小迭代,分别尝试不同的参数,根据需要增加或取消约束,使当前的设计有最好的提高.
每一次循环的开始和结尾都是误差函数值, 标记为ERR.F. 随后显示的是每个视场的XY分量, 虽然总的误差函数值也包含权重因子(例如,如果WTX F4的权重值小, 那么第四个视场中一个大的X分量也不可能会有太大的贡献),但是, 可以让设计者看出哪一个视场或分量对误差函数的作用最大. 接着列出了表面数据和系统的初级基本属性(EFL,缩小倍率REDU, 近轴像高PIM,总长度OAL, 入瞳/出瞳距EN/EX PUP).
最后, 有一个Active Contrains(有效约束, 在这个具体的循环里为10)表. 首先列出EFL, 有目标值, 当前值和他们的差值. 已经知道,这是唯一的特殊约束, 其它所有的约束是什么约束呢? 它们是AUTO已经决定了在这个具体的循环中需要进行控制的一般约束. GL A S1是一个玻璃边界约束(在该例子中, 会想到标有A, B, C的玻璃多边形的边界). Mn ET S1是对表面1的最小厚度的约束.
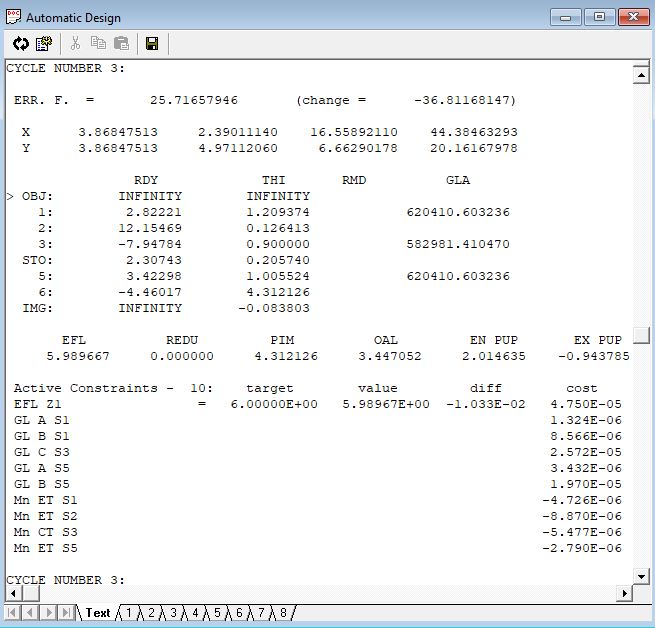
3.5.4.约束的代价
该程序根据Largrange系数的值,动态的决定了每一次循环中需要控制的约束, 并被列在cost栏. 为什么被称为COST? 当一个边界条件被控制时, 程序会受到约束, 趋于使误差函数达到可能是比较低的解空间点(一组变量值). 这个使误差函数无法达到最佳点的约束将会使设计者由于无法实现本来可以实现的误差函数而付出代价(如果可以被释放, 则误差函数可能会更小).
某些约束可能会比其他约束更难控制, 而且要付出更大的代价. 尽管不能直接比较不同类型约束的代价, 但是比较大的值要比较小的值付出的代价要大, 如果您看到了非常大的值(任何正的幂指数, 如1E+02), 那么这个约束正在造成一个大的问题. 或许, 你需要删除它, 或许提供另外的变量,使它比较容易满足.
Largrange乘数的值和符号, 与其它的程序数据一起被用来确定一次循环中哪个约束需要被控制. 剩下的变量(在本次循环中是18-10=8)来准备改善成像质量.