光学知事隅

为什么相机镜头拍摄的图像视场(Field of View,FOV)的角落通常比中心更暗？一方面,相机镜头在设计上通常会在图像中引入“渐晕(vignetting)”，这是故意砍掉FOV角落处的光线以消除过多的镜头像差. 但是,众所周知,即使没有渐晕,图像中的角落区域也会变暗,部分原因是所谓的“余弦四次幂定律”[1].

根据这个“定律”, 当镜头将均匀光源的图像投影到屏幕上时, 在没有渐晕的情况下,屏幕从中心到边缘的光通量密度(即单位面积的光功率)视光轴与入射到屏幕的斜光线之间夹角的余弦的四次方而变化.实际上, 这个“定律”并不普遍适用于所有镜头条件[2-10]. 透镜系统中, 改变透镜设计特性可调整图像的照明分布. 下面我们讨论其中迷人的物理原理.

镜头系统中的相对照度

在镜头设计中，人们用镜头的相对照度来表征图像所在屏幕上的照度分布——在任何离轴位置的辐照度（irradiance，即每单位面积的功率）的比上 图像中心的辐照度。在没有刻意渐晕的情况下，镜头在屏幕上产生的相对照明取决于许多因素，包括从光源散射或发射的光线的性质、镜头瞳孔的形状和大小、镜头中的失真 图像，镜头后面（和前面）的倾斜光线角度，以及一个鲜为人知的数量，称为“微分畸变(differential distortion)”。

我们来看一个简单的例子。 图 1 显示了所谓的后风景镜头 – 放置在虹膜后面的单个镜头元件（在镜头设计术语中称为“光圈”）。该物体是一个直径为 200 毫米的均匀圆盘，以光轴为中心，发出波长为 550 纳米的非相干光。 此外，该物体被假定为“朗伯”光源，这是大多数光学设计程序在计算图像的相对照度时假定的条件。

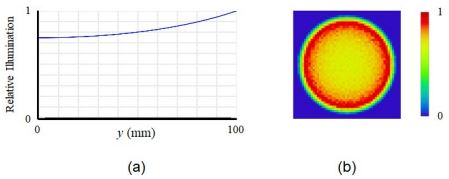
朗伯源发射（或散射）射线，其辐射率（radiance,即单位立体角内每单位源面积的通量）在任何方向上都是恒定的。白色打印纸的表面是这种光源的一个近似例子。该镜头系统的处方在表 1 中给出，您可以在光学设计程序中输入。

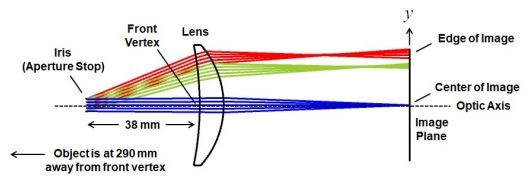
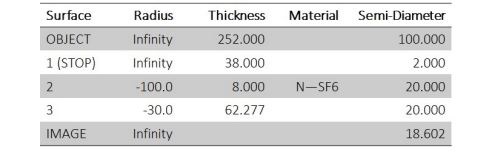
Fig. 2a 显示了该镜头的相对照度图，该图是使用光学设计程序[11]计算得出. 请注意, 相对照度通常被绘制为像所对应物高的函数. 由于物体的全径为 200mm. 因此其光轴上方的高度为 100 mm, 这是Fig.2a 中沿水平轴的最大值的大小. 很明显Fig.2的中心实际上比边缘更暗！Fig.2b 显示了图像表面辐照度的伪彩色图。请注意，由于像边缘的像差，像最远边缘的辐照度(irradiance)略微变暗（注意图Fig.1 中光轴上方最远 y 位置的大模糊点）。

现在，让我们检查在镜头前顶点(front vertex)的三个不同位置处放置虹膜(Iris)时，该镜头的相对照度随虹膜位置的变化(Fig. 3-5). 在Fig.3a 中，虹膜保持在与Fig.1 相同的位置，产生Fig.3b 所示的相对照明(与Fig.2a 相同).

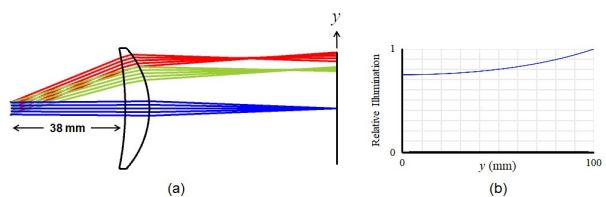
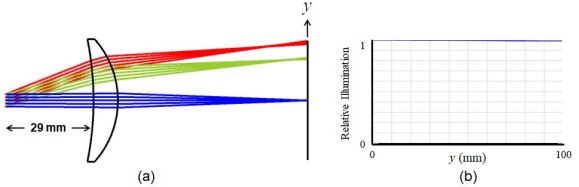
在Fig.4a 中, 虹膜距镜头前顶点 29mm(请注意，从物体到镜头前顶点的总距离一直保持在 290mm), 产生Fig.4b 所示的相对照明.

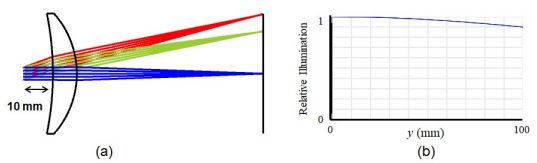
在Fig.5a 中, 虹膜更靠近镜头,距离镜头前顶点 10mm(同时继续将物距与镜头前顶点的距离保持在 290mm), 得到所示的相对照度图Fig.5b. 可见, 通过对虹膜位置的简单操作, 可以调整该镜头的相对照度.

相对照明背后的原理

让我们尝试根据相对照明背后的原理来理解Fig.2-5 中的结果. 一般原则是，由于镜头系统中存在虹膜，因此会产生镜头系统所谓的“入瞳和出瞳”。入瞳是从物体的角度看虹膜的样子，而出瞳是从图像的角度看虹膜的样子。光线穿过入瞳和出瞳的几何形状产生了所观察到的相对照明形式. 这种光线几何的技术术语是“投影立体角”.

从像的观点来看, 当人们从光轴向上(即沿Fig.1 所示的 y 方向)观察出瞳时, 位于虹膜和图像之间的透镜元件可以改变出瞳的外观形状和大小; 它可以产生较小或较大的通量, 穿过光轴上方的出瞳. 因此,每当通量较大时(如Fig.2-3 所示),相对照度从中心到边缘增加, 而当通量较小时, 相对照度会降低. 但是, 当出瞳的形状和大小与入射到图像的光线倾斜度的影响相匹配时, 可以使相对照度保持不变(Fig.4).

光学设计程序通常应用数值算法根据出瞳处的光线几何形状计算相对照明[12]. 由于能量守恒定律(即通过入瞳的光通量等于通过出瞳的光通量), 相对照度也可以根据入瞳处的光线几何形状计算. 事实上, 可以看出[10,13], 在光圈直径较小(即f/数较大或数值孔径较小)的情况下, 应用Fig.6所示的光线几何, 透镜系统的相对照度可以通过以下等式来近似:

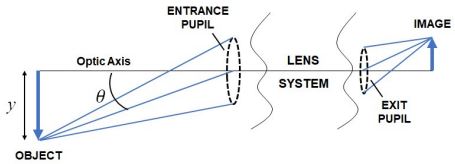
Eq.1中, 离轴点y处对应的入瞳面积比上轴上点对应的入瞳面积.D 是图像畸变(例如, 如果图像畸变为 -10%, 则 D = -0.1). dD/dy 量被称为微分畸变. 它是图像畸变相对于光轴上方物体高度的瞬时变化率. 由于微分畸变,图像中任何位置的相对照度都会受到图像畸变变化的影响, 即使该位置的图像畸变本身为零.

让我们将Eq.(1) 应用于Fig.3 – 5 并将计算结果与这些图中提供的相对照明图进行比较. 在上述三个图中, 虹膜和物体之间都没有透镜元件, 因此比率(即,在这种情况下, 虹膜是入瞳). 将Fig.3 中的镜头系统条件应用于光学设计程序将得到 θ=21.644°, D=-0.145, dD/dy= -0.002907/mm. 将这些值带入Eq.1中可得在全物高处R(y)≈1.55. 根据Fig.3b, 图中的相对照度读数 ≈1/0.75 ≈ 1.33, 所以我们的计算接近这个值(注意图中的相对照度总是对峰值归一化的).

将Fig.4 中的条件应用到光线追踪程序中, 得到θ=20.964°, D=-0.006, dD/dy= -0.001249/mm. 将这些值带入Eq.1中可得R(y)≈1.01; 这似乎接近Fig.4b 中所示的相对照度的最大值. 最后, 根据Fig.5中的条件可得θ=19.654°, D=-0.033, dD/dy= -0.0006312/mm. 将这些值带入Eq.1中可得R(y)≈0.9; 这接近于Fig.5b 所示的全物高处的相对照度.

因此, 该方程非常有效, 证明相对照度可以被视为入射光瞳或出射光瞳处的光线几何形状的函数. 此外,很明显,微分畸变dD/dy在镜头系统的相对照度中起着重要作用.

投影和机器视觉中的相对照度

投影和机器视觉系统中的相对照度通常是镜头和系统变量的更复杂函数. 例如,在投影仪中设计照明子系统时, 通常会使用光学组件, 例如聚光器, 光导管和透镜阵列(也称为“蝇眼透镜(fly’s eye lenses)”). 聚光器用于收集来自光源的尽可能多的光通量, 而光导管(light pipes)和透镜阵列用于使投影目标平面上的照明分布均匀.

在照明设计的其他一些情况下,光学元件的表面可以采用任何形状,这种“自由曲面(Freeform)”透镜和反射镜几乎可以在屏幕上产生任何所需的辐照度(irradiance)分布. 结果是此类系统的相对照明不能由方Eq.(1) 描述,也不是出瞳光线几何形状的简单函数; 而是最好使用照明工程和非成像光学方法来描述屏幕上的辐照度分布[14-17].

在机器视觉系统中, 镜头在电子阵列传感器上形成图像, 例如 CMOS 图像传感器, 其像素前通常组装有微透镜. 因此, 此类系统中的光线可能会在视野边缘被微透镜削波, 除非成像透镜的倾斜光线角度已设计为与微透镜的特定几何形状相匹配[18]. 此外,在机器视觉系统中, 通常在成像镜头旁边安装光源, 以照亮视觉系统感兴趣的区域(ROI,region of interest). 例如,可以在相机镜头周围安装 LED 环, 并且可以排布LED来平衡由镜头设计造成的固有相对照明分布. 因此,图像上的最终辐照度分布可以通过几乎无限的照明几何排列来调整.

余弦四次幂定律在哪里适用？

只有一种情况可以应用余弦四次幂定律. 在光学辐射测量(radiometry)中, 来自小朗伯源的屏幕上的辐照度确实遵循四次方余弦规则(Fig. 7). “小”是指源的表面积明显小于源到屏幕的距离. 在这种情况下, 屏幕上的辐照度(irradiance) E(θ) 可以通过以下等式很好地描述:

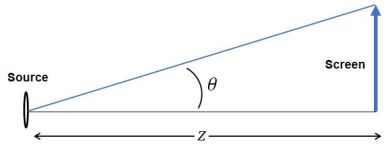
在Eq.2中,L 是光源的辐射率, A 是光源的表面积. 由于已知Eq(2)中的量L在无损光学系统中是不变的,因此从像的观点来看, 成像镜头的出瞳表现为朗伯源[19]. 这是非常准确的, 只要我们将出瞳视为从整个像平面不同的点观看时形状和大小各异的朗伯源. 不幸的是, 这有时也会导致误解,即图像平面上的相对照明将由Eq(2) 描述.

但是，正如我们在本文中看到的，这个简单的余弦规则通常不适用于镜头系统. 透镜系统的相对照度是光源发射特性,入瞳和出瞳的形状和大小,光线相对于光轴的倾斜度,图像畸变以及与图像微分畸变的函数.

参考文献

[1]. R. Kingslake, Optics in Photography, (SPIE Press, 1992), p. 121.

[2]. R. Kingslake, Optics in Photography, (SPIE Press, 1992), p. 122.

[3]. P. Foote, “Illumination from a radiating disk,” in Bulletin of the Bureau of Standards 12, pp.583 – 586 (1915).

[4].M. Reiss, “The Cos^4 Law of Illumination,” J. Opt. Soc. Am. 35(4), pp. 283 – 288 (1945).

[5].G. Slussareff, “A Reply to Max Reiss,” J. Opt. Soc. Am. 36(12), p. 707 (1946).

[6].I. C. Gardner, “Validity of the Cosine-Fourth Power Law of Illumination,” J. Res. Net. Bur.Stand. 39, pp. 213 – 219 (1947).

[7].M. Reiss, “Notes on the Cos^4 Law of Illumination,” J. Opt. Soc. Am. 38(11), pp. 980 – 986(1948).

[8].F. Wachendorf, “The Condition of Equal Irradiance and the Distribution of Light in Images Formed by Optical Systems Without Artificial Vignetting,” J. Opt. Soc. Am. 43(12), pp. 1205 –1208 (1953).

[9].D. Reshidko and J. Sasian, “Role of aberrations in the relative illumination of a lens system,”Opt. Eng. 55(11), 115105 (2016).

[10].R. Siew, “Relative illumination and image distortion,” Opt. Eng. 56(4), 049701 (2017).

[11]. Use ResRays optical software for ray trace.

[12].M. P. Rimmer, “Relative Illumination Calculations,” in Optical System Design, Analysis,Production for Advanced Technology Systems, R. E. Fischer and P. J. Rogers (editors), Proc. SPIE
0655 (1986).

[13].R. Siew, Perspectives on Modern Optics and Imaging: With Practical Examples Using Zemax® OpticStudio®, (2017), pp. 116 – 122.

[14].A. V. Arecchi, T. Messadi, and R. J. Koshel, Field Guide to Illumination, (SPIE, 2007).

[15].R. J. Koshel, Illumination Engineering: Design with Nonimaging Optics, (Wiley, 2013).

[16].J. Chaves, Introduction to Nonimaging Optics, (CRC Press, 2016).

[17].R. Winston, J. C. Minano, and P. Benitez, with contributions by N. Shatz and J. C. Bortz, Nonimaging Optics, (Elsevier, 2005).

[18].P. P. Clark, “Lens Design and Advanced Function for Mobile Cameras,” in Smart MiniCameras, T. V. Galstian, ed., (CRC Press, 2014), p. 12.

[19].R. W. Boyd, Radiometry and the Detection of Optical Radiation, (Wiley, 1983), pp.84 – 85.